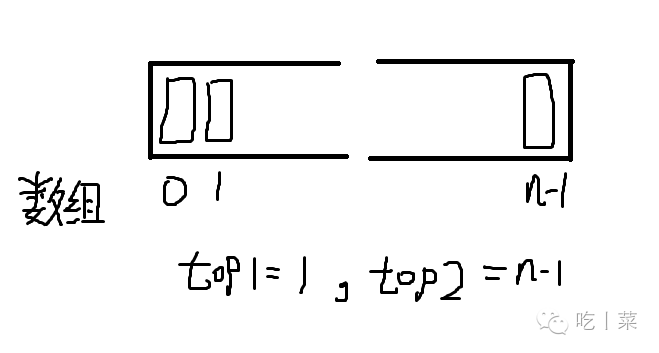- A+
栈也是一种线性结构
它是一种受限的线性表
用于解决一些特殊的问题
如浏览器的回退功能
各种编辑软件的撤销功能等
它是一种后进先出的数据结构
栈(Stack)是限定仅在表尾进行插入和删除操作的线性表
允许插入和删除的一端叫做栈顶(Top),另一端就叫做栈底(bottom)
栈的插入操作叫做进栈,压栈,入栈
栈的删除操作叫做出栈,弹栈
栈的顺序存储结构
|
1 2 3 4 5 6 7 8 9 10 11 |
//栈的顺序存储结构 class StackList<T> { //用于记录栈顶的下标 //-1表示空栈 private int _top = -1; private int _currentLength = 0; private int _maxLength = 24; private T[] _data; |
用一个数组用来保存栈的数据
用数组的尾部来存放栈顶
(如果用头部存放,那么每次出栈都需要移动数据)
定义一个top变量指向栈顶元素的数组下标
栈的顺序存储结构
|
1 2 3 4 5 6 7 8 9 10 |
public StackList() { _data = new T[this._maxLength]; } public StackList(int length) { if (length > 0) { this._maxLength = length; } _data = new T[this._maxLength]; } |
初始化数组的大小(栈的大小)
这里没什么好说的
栈的顺序存储结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
//入栈操作 public bool Push(T element) { if (this._currentLength >= this._maxLength) { Console.WriteLine("栈的空间已满!"); return false; } this._top++; this._data[this._top] = element; this._currentLength++; return true; } |
入栈操作
①先判断数组(栈)是否已经满了
②如果没有满,则将栈顶指标向后移动一位,指向空位置
③在空位置上填入数据
④栈的长度+1,
栈的顺序存储结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
//出栈操作 public bool Pop(ref T element) { if (_top == -1) { Console.WriteLine("栈顶元素为空!"); return false; } element = this._data[this._top]; this._data[this._top] = default(T); this._top--; this._currentLength--; return true; } |
出栈操作
①判断栈是否为空
②用栈顶指标取出栈顶元素
③删除栈顶元素
④栈顶指标减1,指向下一个元素
⑤栈的长度减1
栈的顺序存储结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
//获取栈顶元素,不删除 public bool GetTop(ref T element) { if (_top == -1) { Console.WriteLine("栈顶元素为空!"); return false; } element = this._data[this._top]; return true; } //是否为空 public bool isEmpty() { if (this._top == -1) { return true; } return false; } //清空栈 public bool ClearStack() { for (int i = this._currentLength-1; i >= 0; i--) { this._data[i] = default(T); } this._top = -1; this._currentLength = 0; return true; } //获取栈的长度 public int GetLength() { return this._currentLength; } //获取栈的最大长度 public int GetMaxLength() { return this._maxLength; } |
上面这些看看就好了
不难,很容易理解
两栈共享空间
当有两个栈的空间需求有相反关系时,一个栈的增加
另一个栈就会减少
使用这样的数据结构就非常好
两栈共享空间
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
//两栈共享内存 class DoubleStackList<T> { //_topA为-1时,栈A我空 //_topB为数组最大长度时,栈B为空 private int _topA; private int _topB; private int _currentLengthA = 0; private int _currentLengthB = 0; private int _maxLength = 24; private T[] _data; |
定义变量们
两栈共享空间
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
//初始化为两个空栈 public DoubleStackList() { this._data = new T[this._maxLength]; this._topA = -1; this._topB = this._maxLength; } public DoubleStackList(int length) { if (length > 0) { this._maxLength = length; } this._data = new T[this._maxLength]; this._topA = -1; this._topB = this._maxLength; } |
初始化两个空栈
两栈共享空间
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//入栈操作A public bool PushA(T element) { if (this._topB == this._topA + 1) { Console.WriteLine("共享的空间已满!"); return false; } this._topA++; this._data[this._topA] = element; this._currentLengthA++; return true; } //入栈操作B public bool PushB(T element) { if (this._topB == this._topA + 1) { Console.WriteLine("共享的空间已满!"); return false; } this._topB--; this._data[this._topB] = element; this._currentLengthB++; return true; } |
可以参考上面栈的顺序存储结构的入栈操作
这里不同的是栈A是由数组头部向后一直添加
栈B是右数组尾部向前一直添加
两个指标相差一个就说明空间已满
两栈共享空间
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
//出栈操作A public bool PopA(ref T element) { if (this._topA == -1) { Console.WriteLine("栈A为空!!"); return false; } element = this._data[this._topA]; this._data[this._topA] = default(T); this._topA--; this._currentLengthA--; return true; } //出栈操作B public bool PopB(ref T element) { if (this._topB == this._maxLength) { Console.WriteLine("栈B为空!!"); return false; } element = this._data[this._topB]; this._data[this._topB] = default(T); this._topB++; this._currentLengthB--; return true; } |
同样的就不细说了
两个栈的的出栈方向就与入栈操作方向相反就行了
链式存储结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
//栈的链式存储结构 class StackLink<T> { class Node { public T data; public Node next; } //栈顶指向链表的第一个结点 private Node _top; private int _currentLenth = 0; //构造空链表 public StackLink() { this._top = null; } |
定义栈顶为链表的头部
然后就只能在链表的头部进行插入和删除操作
这样就是栈的链式存储结构了
注意_top指向的是栈顶(链表的第一个结点,不是头结点了)
这里不需要头结点了
当_top为null是,则为空栈
链式存储结构
|
1 2 3 4 5 6 7 8 9 10 11 |
//进栈操作 public bool Push(T element) { Node addNode = new Node(); addNode.data = element; addNode.next = this._top; this._top = addNode; this._currentLenth++; return true; } |
链式结构的进栈操作
①新建结点,赋值数值,记下一个结点为当前的栈顶
②设置当前栈顶为新加结点
③栈的长度+1
链式存储结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//出栈操作 public bool Pop(ref T element) { if (this._top == null) { Console.WriteLine("该栈为空!"); return false; } Node deleteNode = this._top; element = deleteNode.data; this._top = deleteNode.next; deleteNode = null; this._currentLenth--; return true; } |
出栈操作
①判断栈是否为空
②得到栈顶结点,取出栈顶的数值
③设置栈顶为当前栈顶的下一个结点
④栈的长度-1
链式存储结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
//清空栈 public bool ClearStack() { Node deleteNode = this._top; while (deleteNode != null) { //这样写其实没有必要,这里只是为了突出删除 //c#的堆内存如果没有变量引用的话,它是会被GC回收的 Node goNode = deleteNode.next; deleteNode = null; deleteNode = goNode; } this._top = null; this._currentLenth = 0; return true; } |
(请无视最后一条注释!!!)
自己看吧
就是不停的取出栈顶,然后删除
直到栈顶为空时
测试栈的顺序存储结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
static void TestStackList() { //进栈测试 StackList<int> s = new StackList<int>(); PrintStackList(s, "进栈前:"); s.Push(5); s.Push(20); s.Push(33); PrintStackList(s, "依次进栈5,20,33后依次出栈:"); Console.WriteLine(s.isEmpty()); Console.WriteLine(); //清空栈 s.Push(99); s.Push(88); s.Push(22); s.ClearStack(); PrintStackList(s, "清空栈后:"); } static void PrintStackList(StackList<int> s, string text = "输出:") { int data = 0; int length = s.GetLength(); Console.Write(text); for (int i = 0; i < length; i++) { s.Pop(ref data); Console.Write(data.ToString() + " "); } Console.WriteLine(); } |
测试两栈共享空间
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
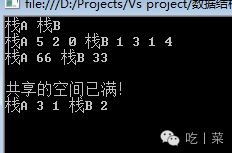
static void TestDoubleStackList() { //入栈 DoubleStackList<int> d = new DoubleStackList<int>(); PrintDoubleStackList(d, "入栈前:"); d.PushA(0); d.PushA(2); d.PushA(5); d.PushB(4); d.PushB(1); d.PushB(3); d.PushB(1); PrintDoubleStackList(d, "入栈后出栈输出:"); d.PushA(66); d.PushB(33); PrintDoubleStackList(d, "再次入栈测试出栈:"); Console.WriteLine(); //测试栈满 DoubleStackList<int> dd = new DoubleStackList<int>(3); dd.PushA(1); dd.PushB(2); dd.PushA(3); dd.PushA(66); PrintDoubleStackList(dd); } static void PrintDoubleStackList(DoubleStackList<int> d, string text = "输出:") { //输出A栈 int element = 0; int length = d.GetLengthA(); Console.Write("栈A "); for (int i = 0; i < length; i++) { d.PopA(ref element); Console.Write(element.ToString() + " "); } //栈B出栈并输出 length = d.GetLengthB(); Console.Write("栈B "); for (int i = 0; i < length; i++) { d.PopB(ref element); Console.Write(element.ToString() + " "); } Console.WriteLine(); } |
测试栈的链式存储结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
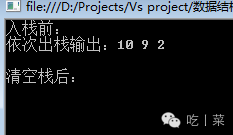
static void TestStackLink() { //入栈 StackLink<int> s = new StackLink<int>(); PrintStackLink(s, "入栈前:"); s.Push(2); s.Push(9); s.Push(10); PrintStackLink(s, "依次出栈输出:"); Console.WriteLine(); //清空栈测试 s.Push(100); s.Push(200); s.ClearStack(); PrintStackLink(s, "清空栈后:"); } static void PrintStackLink(StackLink<int> s, string text = "输出:") { int element = 0; int length = s.GetLength(); Console.Write(text); for (int i = 0; i < length; i++) { s.Pop(ref element); Console.Write(element.ToString() + " "); } Console.WriteLine(); } |