- A+
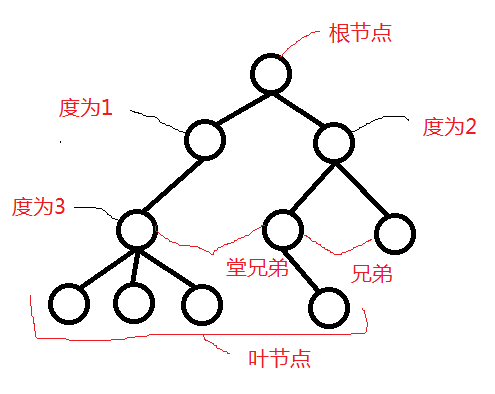
在前面的数据存储结构都是线性的,也就是一对一连着的,到了树形结构就是一对多的结构了,就像是一颗树那样,它只有一根主干(根节点),主干上长有很多树枝,树枝上又有很多枝杈,枝杈上又有很多树叶(叶结点)
很明显的没有孩子的为叶节点,度的值为当前节点孩子的个数,深第为4,为树的层数,下面开始写写这种结构
一、先做准备运动
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
class MyTree<T> { public class Node { public MyTree<T> tree = null; public T data = default(T); public Node[] childs = null; public Node(MyTree<T> tree) { this.tree = tree; } public void ValueTo(T data) { this.data = data; } } |
这个是存储树结点数据的结构,首先tree为表明它这个结点是属于哪一颗树的。因为我设计成结点是可以通过外面访问的,若要对它操作,我起码也要知道它是哪颗树的吧。data就是数据域了,用来保存数据的,数组childs是用来保存子节点的,构造函数Node必须指定它是属于哪棵树的,树都没有,怎么会有结点呢。ValueTo方法用来修改它的数据域的
二、预备运动
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
//头结点,头结点的child[0]就表示根节点 private Node _headNode = null; private int _length = 0; public MyTree() { this._headNode = new Node(this); } //指定根的数据 public MyTree(T data) { this._headNode = new Node(this); Node newNode = new Node(this); newNode.data = data; this._headNode.childs = new Node[1]; this._headNode.childs[0] = newNode; this._length = 1; } |
这里我像线性表那样设置了一个头结点,其实是为了方便操作,设定头结点有且只有一个子节点,这就是根节点,_length用来保存树的结点个数,还有两个构造函数,一个构造成空树,一个构造成只有一个根节点的树
三、创建树的根
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//创建树的根 public bool CreatRoot(T data) { if (!this.isEmpty()) { Console.WriteLine("树的根已存在,不需要重新创建!"); return false; } Node root = new Node(this); root.data = data; this._headNode.childs = new Node[1]; this._headNode.childs[0] = root; this._length = 1; return true; } |
这个方法是为了那些空树用来创建根节点的,在创建根节点前,首先要判断一下是否已经存在了根节点,然后就只需要创建根节点,赋值数据,再将它的引用赋值给头结点的子节点数组第一位,最后将长度设置为1
四、添加结点
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
//为指定结点添加子节点 public void AddNodeTo(Node toNode, T data) { if (!this.isMyNode(toNode)){ Console.WriteLine("你所操作的结点不是本树的结点!"); return; } Node addNode = new Node(this); addNode.data = data; Node[] temp = toNode.childs; int childLength = (temp == null ? 1 : temp.Length + 1); toNode.childs = new Node[childLength]; int i = 0; for (; i < childLength-1; i++) { toNode.childs[i] = temp[i]; } toNode.childs[i] = addNode; this._length++; } |
为指定的结点添加结点,首先判断一下要添加的目标结点是不是本树的结点,如果不属于自己的结点,那就没有权利去操作它了,新建结点addNode,并赋值数据,先临时保存一下目标结点的所有子节点,然后确定扩展后子节点数组的长度,重构目标结点的子节点数组,然后依次赋值,将新加的结点放到最后面,再将长度+1
|
1 2 3 4 5 6 7 8 9 10 |
//为指定位置的结点添加子节点 public void AddNodeTo(int index, T data) { if (!this._checkIndex(index)){ Console.WriteLine("目标位置的结点不存在!"); return; } Node toNode = this.GetNodeByIndex(index); this.AddNodeTo(toNode, data); } |
这个是通过索引来为目标结点添加子节点,首先需要判断索引的合法性,再用索引来找到目标结点,再用AddNodeTo()方法添加子节点
五、返回指定位置的结点
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//返回指定位置的结点 public Node GetNodeByIndex(int index) { if (!this._checkIndex(index)) { Console.WriteLine("索引错误!"); return null; } if (this.isEmpty()) { Console.WriteLine("此树为空树!"); return null; } //将头结点加入到队列中 Queue<Node> q = new Queue<Node>(); q.Enqueue(this._headNode.childs[0]); int goindex = 1; Node goNode = this._headNode; while (goindex < index) { goNode = q.Dequeue(); int nodeLength = goNode.childs.Length; goindex += nodeLength; for (int i = 0; i < nodeLength; i++) { q.Enqueue(goNode.childs[i]); } } int sub = goNode.childs.Length - goindex + index - 1; return goNode.childs[sub]; } |
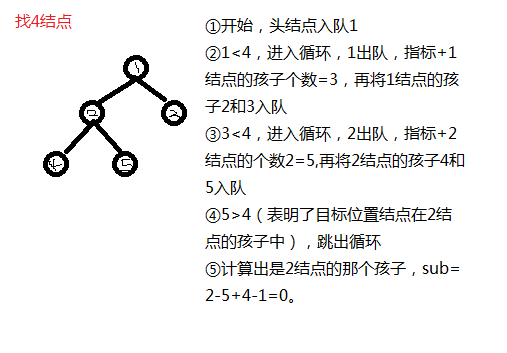
通过索引来获取到指定的结点,首先涉及到索引,就必须要检查索引的合法性,还要判断一下树是否为空,索引的大小是依照从上层往下层,每层从左往右递增,然后看图吧,涉及层操作,用队列把它变成线性的
六、删除目标位置的结点和其子结点
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
//删除目标位置的结点及其子节点 public void DeleteByIndex(int index) { if (!this._checkIndex(index)){ Console.WriteLine("索引错误!"); return; } if (index == 1) { //删除树的根,就是删除整棵树 this._headNode.childs[0] = null; this._length = 0; return; } int local = 0; Node goNode = this.GetNodeParentAndLocalByIndex(index, ref local); if (goNode == null) { Console.WriteLine("删除失败,请检查索引是否正确!"); return; } //删除双亲结点对目标子节点的引用,表示删除 Node[] temp = goNode.childs; goNode.childs = new Node[temp.Length - 1]; for (int i = 0; i < temp.Length; i++) { if (i < local - 1) { goNode.childs[i] = temp[i]; } else if (i > local - 1) { goNode.childs[i - 1] = temp[i]; } } this._length--; } |
通过索引删除删除结点,首先的要检查索引的合法性,如果要删除1结点,也就是根节点,那么直接清空整棵树就好了,要删除一个结点,就必须找到它的父节点,删除掉对它的引用,通过GetNodeParentAndLocalByIndex方法,找到它的父节点和所在引用数组中的位置,先用临时结点数组保存子节点数组的引用,重构子节点数组的大小-1,除去对删除结点的引用。最后,结点长度-1
七、返回指定位置的父节点及其索引
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
//返回指定位置结点的父节点及其 它为第几位 public Node GetNodeParentAndLocalByIndex(int index,ref int local) { if (!this._checkIndex(index)) { Console.WriteLine("索引错误!"); return null; } if (index == 1) { //根节点没有双亲 Console.WriteLine("根节点没有双亲!"); return null; } if (this.isEmpty()) { Console.WriteLine("此树为空树!"); return null; } //将头结点加入到队列中 Queue<Node> q = new Queue<Node>(); q.Enqueue(this._headNode.childs[0]); int goindex = 1; Node goNode = this._headNode; while (goindex < index) { goNode = q.Dequeue(); int nodeLength = goNode.childs.Length; goindex += nodeLength; for (int i = 0; i < nodeLength; i++) { q.Enqueue(goNode.childs[i]); } } local = goNode.childs.Length - goindex + index ; return goNode; } |
首先,判断索引的合法性,是否为根节点,是否为空树,后面使用队列,参考GetNodeByIndex方法(一样的,哈哈)
八、层次遍历树,存储为数组
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
//层次遍历返回数组 public T[] GetDatasByLevels() { if (this.isEmpty()) { Console.WriteLine("树为空树!"); return null; } Queue<Node> q = new Queue<Node>(); q.Enqueue(this._headNode.childs[0]); Node goNode = null; T[] datas = new T[this._length]; int goIndex = 0; while (q.Count != 0) { goNode = q.Dequeue(); datas[goIndex] = goNode.data; int num = goNode.childs == null ? 0 : goNode.childs.Length; for (int i = 0; i < num; i++) { q.Enqueue(goNode.childs[i]); } goIndex++; } return datas; } |
将树按层遍历转换成数组,同理用队列的方式,将所有结点入队,再每个出队,赋值给数组数组,用goIndex作为指标,再返回数据数组
九、获得树的高度
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
//返回树的高度 public int GetHeight() { if (this.isEmpty()) { Console.WriteLine("此树为空!"); return 0; } int height = 0; Queue<Node> q = new Queue<Node>(); q.Enqueue(this._headNode.childs[0]);//根结点入队列 int count1 = 1; int count2 = 1; Node temp; while (count2 != 0) { height++; count2 = 0; for (int i = 0; i < count1; i++) { temp = q.Dequeue(); if (temp.childs != null) { count2 += temp.childs.Length; for (int j = 0; j < temp.childs.Length; j++) { q.Enqueue(temp.childs[j]); } } } count1 = count2; } return height; } |
计算树的高度,首先检查树是否为空,再用队列用来保存每一层的结点,count变量是用来保存每层结点的个数,队列出入队都以层为单位。每一次出队,树的高度都加1
十、其他的方法
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
//判断是否为空树 public bool isEmpty() { if (this._headNode.childs == null) { return true; } return false; } //检查是否为该树的结点 public bool isMyNode(Node target) { if (target.tree == this) { return true; } return false; } //检查索引是否合法 private bool _checkIndex(int index) { if (index < 1 || index > this.GetLength()) { return false; } return true; } //清空树 public void Clear() { this._headNode.childs = null; this._length = 0; } //获取指定位置的数据 public T GetElementByIndex(int index) { Node target = this.GetNodeByIndex(index); if (target != null) { return target.data; } Console.WriteLine("获取结点数据出错!"); return default(T); } //返回结点的个数 public int GetLength() { return this._length; } |
十一、测试
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
static public void TestMyTree() { MyTree<int> t = new MyTree<int>(1); PrintfMyTree(t, "添加多个结点前:"); t.AddNodeTo(1, 2); t.AddNodeTo(1, 3); t.AddNodeTo(2, 4); t.AddNodeTo(2, 5); t.AddNodeTo(3, 6); PrintfMyTree(t,"添加多个结点后:"); Console.WriteLine("树结点的个数为:" + t.GetLength()); Console.WriteLine(); t.DeleteByIndex(4); PrintfMyTree(t,"删除第四个结点后:"); Console.WriteLine("树结点的个数为:" + t.GetLength()); Console.WriteLine(); MyTree<int>.Node node1 = t.GetNodeByIndex(3); Console.WriteLine("第三个结点的数据为:" + node1.data); MyTree<int>.Node node2 = t.GetNodeByIndex(4); Console.WriteLine("第四个结点的数据为:"+node2.data); Console.WriteLine(); int local = 0; MyTree<int>.Node node3 = t.GetNodeParentAndLocalByIndex(5, ref local); Console.WriteLine("第5个结点的双亲数据为:" + node3.data + ",位置为:" + local); MyTree<int>.Node node4 = t.GetNodeParentAndLocalByIndex(3, ref local); Console.WriteLine("第3个结点的双亲数据为:" + node4.data + ",位置为:" + local); Console.WriteLine("树的高度为!" + t.GetHeight()); Console.WriteLine(); Console.WriteLine("第1个结点的数据为:" + t.GetElementByIndex(1)); Console.WriteLine("第2个结点的数据为:" + t.GetElementByIndex(2)); Console.WriteLine(); t.Clear(); PrintfMyTree(t, "清空树后:"); t.CreatRoot(100); PrintfMyTree(t, "创建根节点后:"); Console.WriteLine("树的高度为!" + t.GetHeight()); } static public void PrintfMyTree(MyTree<int> t,string text = "输出为:") { Console.Write(text); int[] datas = t.GetDatasByLevels(); if (datas != null) { for (int i = 0; i < datas.Length; i++) { Console.Write(datas[i] + " "); } } Console.WriteLine(); } |
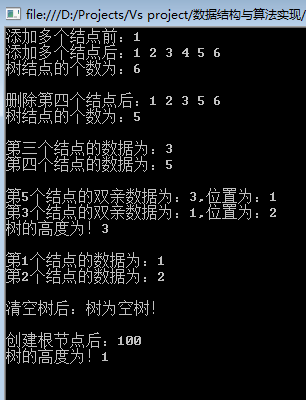
十二、结果