- A+
向量,具有大小和方向
在虚幻的空间坐标中
三维向量表示为(x ,y , z)
它由两个点确定
例如:A(2,2,3), B(3,1,5) (空间坐标点)
则向量AB = (3-2,1-2,5-3) = (1,-1,2)
方向就是A指向B
向量的加减乘除法
他们的运算方法其实就是对应其各个分量的运算
例如 加法
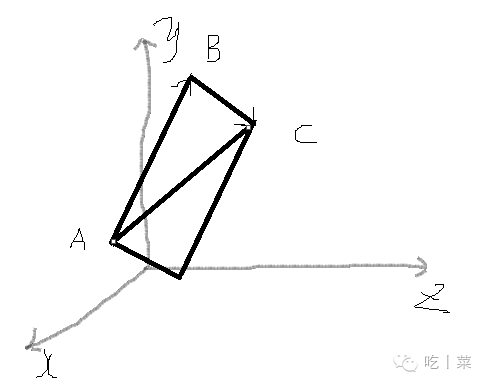
A(1,1,2),B(3,6,1),C(1,5,3)
则AB = (2,5,-1) BC = (-2,-1,2) AC = (0,4,1)
AB + BC = (2-2,5-1,-1+2) = (0,4,1) = AC
相加得到的向量就是平移原来两条向量形成的平行四边形的长对角线
由起点指向踪点,沿着路径
减法
AB = (2,5,-1),AC = (0,4,1), CB = (2,1,-2)
AB - AC = (2-0,5-4,-1-1) = (2,1,-2) = CB
得到的的向量就是平移原来两条向量形成的平行四边形的短对角线
由减数(-号后面那个数)指向被减数
乘除法就是将对应分量乘除于对应的数。
向量的模于单位化
已知 向量AB = (2,5,-1)
则|AB| = √(2²+5²+(-1)²) = √(30)
模|AB|其实就是向量的长度
而要将向量单位化,只要将向量的分量分别除以向量的长度
AB(单位向量) = (2/|AB|,5/|AB|,(-1)/|AB|)
单位向量的模的大小为1,这样一来就可以很好的表达其方向了
向量的点积
AB = (2,5,-1),AC = (0,4,1)
AB · AC = 2×0 + 5×4 + (-1)×1 = 19
这样看并没有什么意义
结合公式:AB · AC = |AB||AC|cosΘ
可以求出cosΘ的值,推导出该两个向量的夹角
向量的叉积
AB = (2,5,-1),AC = (0,4,1)
AB × AC = (5×1-4×-1,-1×0-1×2,2×4-0×5) = (9,-2,8)
技巧:计算分量x时,排除两向量的x分量
采用第一个向量的x下一个分量(y)
乘于第二个向量的对应分量(y)的下一个分量z
再减去相应的另外两个分量的积
已知两条向量可以确定一个平面
已知叉积的几何意义是求该平面的法向量
也就是说(9,-2,8)垂直于AB和AC
用点积验证
AB · (9,-2,8) = 2×9 + 5×(-2)+ (-1)×8 = 0
AC· (9,-2,8) = 0×9 + 4×(-2)+ 1×8 = 0
已知cos(90°) = 0
所以它们的夹角为90°