- A+
串其实就是字符串,字符串其实就是由字符组成的有限序列,同线性表差不多,只不过它的元素为字符了,但是不同的是,线性表注重的是单个元素的操作,而串一般都是对多个元素的操作
有的字符串以字符‘\0’表示结束,0下标数值元素存储字符串的长度。这里因为c#的数组是Array派生,它是需要实例化的,是个引用,我们可以为它赋予一个新的空间,所以这里将使用数组长度来约束字符串,得知它的结尾就是最后一个元素,字符串的长度就是数组的长度,下面开始实现。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//串的顺序存储结构 class StringList { private char[] _data; public StringList(char[] chars) { this.ValueTo(chars); } //创建空串 public StringList() { this._data = null; } //串赋值为字符数组 public void ValueTo(char[] chars) { if (chars == null) { this._data = null; return; } this._data = new char[chars.Length]; for (int i = 0; i < chars.Length; i++) { _data[i] = chars[i]; } } |
_data是一个char数组类型。两个构造函数,一个调用ValueTo初始化字符串为chars,一个赋值为null,表示为空字符串,其中ValueTo是用字符数组赋值给_data,初始化或重新分配空间给_data数组,长度为赋值chars的长度,遍历每个char元素赋值给_data的对应位置。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//串赋值为串 public void ValueTo(StringList s) { if (s.isEmpty()) { Console.WriteLine("赋值的字符串不能为空!"); return; } int length = s.Length(); this._data = new char[length]; char c = default(char); for (int i = 0; i < length; i++) { s.GetCharByIndex(i + 1,ref c); this._data[i] = c; } } |
用串来赋值
①先判断s字符串是否为空就是判断数据域_data是否为null
|
1 2 3 4 5 6 7 8 |
//是否为空 public bool isEmpty() { if (this._data == null) { return true; } return false; } |
②获取到s串的长度,重构或初始_data数组的大小
|
1 2 3 4 5 6 7 8 |
//获取长度 public int Length() { if (this.isEmpty()) { return 0; } return this._data.Length; } |
③遍历整个串的长度,通过GetCharByIndex获取对应位置的字符,赋值给_data数据域的对应位置
|
1 2 3 4 5 6 7 8 9 10 |
//获取到指定位置的字符 public bool GetCharByIndex(int index, ref char c) { if (index < 1 || index > this.Length()) { Console.WriteLine("索引错误!"); return false; } c = this._data[index - 1]; return true; } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
//插入字符数组 public bool Insert(int index , char[] chars) { if (this.isEmpty()||chars == null) { Console.WriteLine("插入的字符不能为空!"); return false; } int length = _data.Length; if (index > length || index < 1) { Console.WriteLine("索引位置错误!"); return false; } int cLength = chars.Length; char[] term = _data; _data = new char[length + cLength]; int i = 0; for (; i < index - 1; i++) { _data[i] = term[i]; } for (int j = 0; j < cLength; j++) { _data[i] = chars[j]; i++; } for (int k = index - 1; k < length; k++) { _data[i] = term[k]; i++; } return true; } |
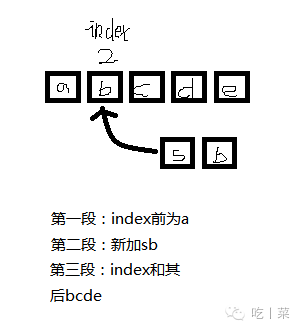
插入字符数组到指定位置
①先判断本串和字符数组是否为空
②判断索引的合法性
③临时保存本串的数据
④重构本串的数据域大小为原串长度+插入字符数组长度
⑤原串index前的字符,插入的字符,原串index和其后的字符,分为三段分别按顺序赋值给新的数据域
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
//删除指定位置长度的字符串 public bool Delete(int index, int length) { if (this.isEmpty()) { Console.WriteLine("被删除的字符串为空!"); return false; } int sounceLength = this._data.Length; if (index < 1 || index > sounceLength || length < 1 || index + length - 1 > sounceLength) { Console.WriteLine("索引位置和长度错误!"); return false; } char[] term = this._data; int newLength = sounceLength - length; this._data = new char[newLength]; int go = 0; for (int i = 0; i < newLength; i++) { if (i == index - 1) { go = length; } this._data[i] = term[i + go]; } return true; } |
删除指定位置长度的字符串
①同样的需要判断串是否为空和索引的合法性
②临时保存原串的数据
③重构数据域大小为删除字符串后的长度
④遍历赋值,通过go位移跳过被删除的元素
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
//复制指定字符数组的指定位置长度的字符 public bool CopyTo(int sounceIndex, char[] copy, int copyIndex = 1, int length = 0) { if (length == 0 && copyIndex > 0) { //复制copy数组copyIndex后面的所有字符 length = copy.Length - copyIndex + 1; } char[] copyChars = this.subChar(copy, copyIndex, length); if (copyChars == null) { return false; } return this.Insert(sounceIndex, copyChars); } //复制串到插入到指定位置 public bool CopyTo(int sounceIndex, StringList s, int copyIndex = 1, int length = 0) { return this.CopyTo(sounceIndex, s.ToChars(), copyIndex, length); } |
这里是截取字符数组或字符串指定位置长度的字符,插入到主串指定位置中
①先判断length是否为0,是的话取length为最长的长度
②截取出指定位置长度的字符
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
//获取子字符数组 private char[] subChar(char[] chars, int index, int length) { if (chars == null) { Console.WriteLine("截取的字符数组为空!"); return null; } int cLength = chars.Length; if (length <1 || index < 1||index > cLength || index + length - 1 > cLength) { Console.WriteLine("索引和长度错误!"); return null; } char[] newChar = new char[length]; for (int i = 0; i < length; i++) { newChar[i] = chars[index - 1 + i]; } return newChar; } |
判断字符数组是否为空,判断位置和长度的合法性,新建length长度的数组,遍历源字符数组,复制指定位置的字符到新数组中,返回
③判断一下截取出来的字符数组是否为空
④将截取出来的字符数组,插入到主串的(这个方法前面讲过),下面那个方法调用有个ToChars()方法,它是将字符串类转换位一个字符数组,并返回
|
1 2 3 4 5 6 7 8 9 10 11 |
//转换为字符数组并返回 public char[] ToChars() { if (this.isEmpty()) { return null; } int sounceLength = this._data.Length; char[] newChar = this.subChar(this._data, 1, sounceLength); return newChar; } |
你会发现,这里也是使用subChar直接截取整个字符数组的
|
1 2 3 4 5 6 7 8 9 10 |
//截取指定位置长度的串,成为一个新的串 public StringList SubString(int index, int length) { char[] sub = this.subChar(this._data, index, length); if (sub == null) { return null; } StringList newString = new StringList(sub); return newString; } |
取出一个子串
①截取出指定位置长度的字符数组
②判断这个字符数组是否为空
③新建一个串,并初始化为这个字符数组
④返回新建的串
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
//链接串s在尾部 public bool Concat(StringList s) { if (this.isEmpty() || s.isEmpty()) { return false; } int length1 = this.Length(); int length2 = s.Length(); char[] term = this._data; this._data = new char[length1 + length2]; int i = 0; for (; i < length1; i++) { this._data[i] = term[i]; } term = s.ToChars(); for (; i < length1 + length2; i++) { this._data[i] = term[i-length1]; } return true; } |
以自身为主串,在尾部链接s串
①判断主串和链接串是否为空
②得出他们的长度
③临时保存主串的字符数据
④重构主串数据域的长度为两串相加的长度
⑤分两段分别赋值为新的数据域,一段是原主串的数据,一段是链接的串的数据
|
1 2 3 4 5 6 7 8 9 10 11 12 |
//链接本串和s串为新串返回 public StringList ConcatToNew(StringList s) { if (this.isEmpty() || s.isEmpty()) { return null; } StringList newString = new StringList(); newString.ValueTo(this); newString.Concat(s); return newString; } |
这个就是调用已经写好的方法,可以参考这些方法
①判断两串是否为空
②新建一个空串
③赋值为本串的字符
④再用新串链接s串
⑤返回新串
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
//普通匹配查找串的位置 public int SimpleIndex(StringList T, int pos = 1) { if (T.isEmpty() || this.isEmpty()) { return 0; } int mainLength = this.Length(); int matchLength = T.Length(); int i; if (pos > 0 && pos <= mainLength) { i = pos; while (i <= mainLength - matchLength + 1) { StringList sub = this.SubString(i, matchLength); if (sub.Compare(T) != 0) { i++; } else { return i; } } } return 0; } //比较两个串 1本串大 -1 s串大 0相等 public int Compare(StringList s) { int sounceLength = this.Length(); int length = s.Length(); int i = 0; int j = 0; char c = '\0'; while (i < sounceLength && j < length) { s.GetCharByIndex(j + 1, ref c); if (this._data[i] > c) { return 1; } if (this._data[i] < c) { return -1; } i++; j++; } if (sounceLength == length) { return 0; } if (sounceLength > length) { return 1; } return -1; } |
通过遍历查找子串的位置,没有找到返回0
①先检查主串和匹配串是否为空
②得到它们的长度
③在指定的主串i = pos位开始
④不断截取出与匹配长度的子串与匹配串比较,直到找到与匹配串相匹配的串,返回它的位置i,或者截取的子串长度小于匹配串长度了
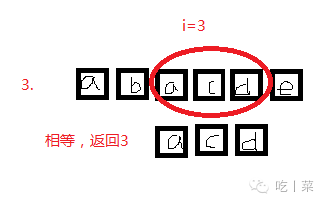
如果字符串很长,匹配的字符串也很长
例如000000000000000000000000000001
匹配00000000000001
这样还是采用朴素的匹配方法的话,需要比较的次数是很多的,每次i的循环比较,都要比较到最后字符才能知道不相等,计算机的数据是0和1的世界,如果使用这种方法是不效率的,是很恐怖的,所以下面是KMP算法。
KMP匹配算法:
!!!KMP算法可以跳过这些没必要比较的循环!!!
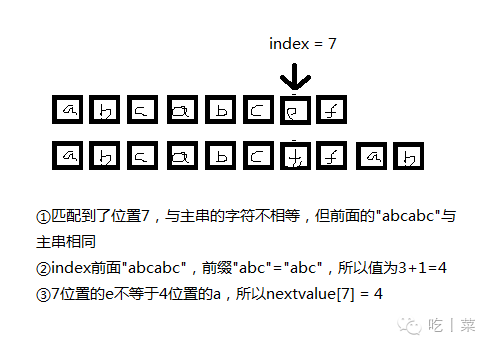
通过匹配串,得出nextvalue[index]数组,index就是匹配不相等的匹配串位置,这里需要得出所有位置,因为你也不知道哪里不匹配,保存的数据就是index位置前面字符串前后缀字符相同个数+1,特殊的index = 1时,值为0
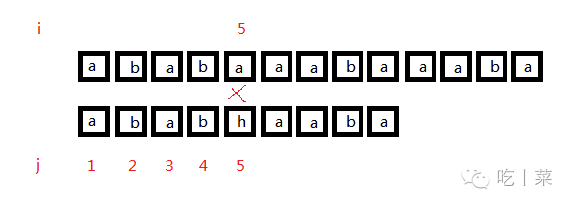
也就是说7号位置匹配不成功后,就跳到四号位,为什么呢,看图
!!!KMP算法可以减少对某次循环中某些相同字符的重复比较!!!
下面看一下nextvalue的求法
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
private void getNextval(StringList T, int[] nextval) { int i, j; //代表第几个字符 i = 1; j = 0; nextval[1] = 0; while (i < T.Length()) { if (j == 0 || T[i] == T[j]) { j++; i++; if (T[i] != T[j]) { nextval[i] = j; } else { nextval[i] = nextval[j]; } } else { j = nextval[j]; } } } |
这里直接说一下例子吧!
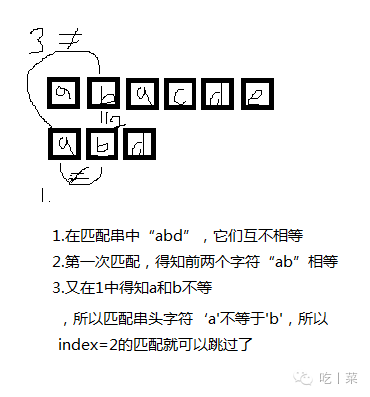
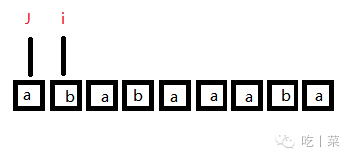
例如匹配串T = "ababaaaba"
①nextval[1] = 0;
②j = 0 : i++=2 , j++ = 1; nextval[2] = 1; 字符串"a"
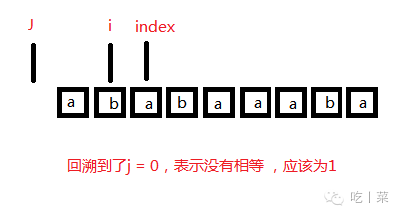
③j = 1,i = 2 ,"a" != "b" : 回溯 j = nextval[j] = 0 字符串"ab",j = 0表示回到了最头部,没有一个相等
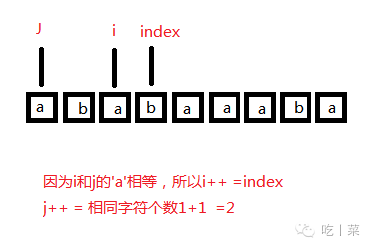
④j = 0 : i++ = 3 , j++ = 1 ;
但因为3和1位置都是'a'。(我3号位的'a'匹配不相等了,那我回到1号位也是'a',也是不相等)。所以这是没必要的,直接回溯到1号位的回溯,nextval[3] = nextval[1] = 0; 字符串"ab"
⑤j=1,i=3,'a'='a' :i++=4,j++=2 ;
同理的4和2的字符也相等,也没必要回溯到2,nextval[4] = nextval[2] = 1;
⑥j=2, i=4, 'b' = 'b' :i++ = 5, j++=3; 5和3的字符相同,则nextval[5] = nextval[3] = 0
⑦j = 3, i = 5 ,'a' = 'a' : i++=6,j++4 ,6和4的字符不相等,可以回溯到4号位则nextval[6] = j = 4。你可以发现,j一直在往后记录着前后缀相同个数+1,而i就是遍历的位置,也可以说是后缀字符
⑧j = 4, i = 6 ,‘b’!='a':有不相等了,j 就会回溯到前面相等的地方,j = nextval[j] = nextval[4] = 1,再来 j = 1,i = 6 ,'a'='a':i++=7,j++=2,7和2的字符不相等,则nextval[7] = 2
⑨往下就不讲了,自己推吧!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
//KMP匹配方法 public int Index(StringList T, int pos = 1) { if (this.isEmpty() || T.isEmpty()) { return 0; } int mainLength = this.Length(); int matchLength = T.Length(); int i = 0; int j = 1; if (pos > 0 && pos <= mainLength) { i = pos; int[] nextval = new int[matchLength + 1]; this.getNextval(T, nextval); while (i <= mainLength && j <= matchLength) { if (j == 0 || this[i] == T[j]) { ++i; ++j; } else { j = nextval[j]; } } } if (j > matchLength) { return i - matchLength; } return 0; } |
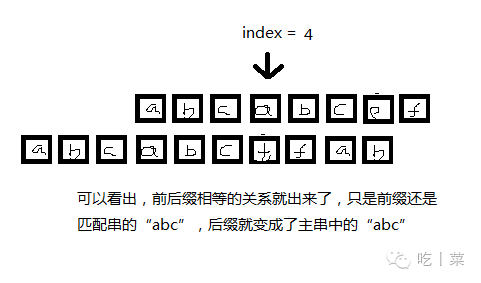
其实这个跟获取nextval数组差不多,同样使用i向后遍历字符,i不会较小,而j就是用来记录字符相同个数+1,如果有某个地方不相同了,就回到上一次有相同的地方
此时5和3相同,主串就可以走向下一轮循环,j也要+1
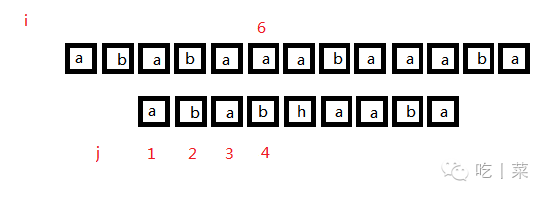
此时4和6不等,j就要回到nextval[4] = 0,表示没有相同的了,可以下一轮循环了
................................
测试
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
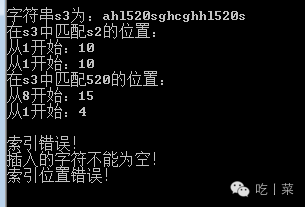
static void TestStringList() { //初始化和赋值 StringList s1 = new StringList(new char[] { 'a', 'b', 'c', 'g', 'h' }); StringList s2 = new StringList(); s2.ValueTo(s1); PrintStringList(s1,"字符串s1:"); PrintStringList(s2, "字符串s2:"); s2.ValueTo(new char[] { 'h', 'l', 's' }); PrintStringList(s2, "s2重新赋值后:"); Console.WriteLine(); //插入和删除操作 PrintStringList(s1, "原s1串:"); s1.Delete(2, 2); PrintStringList(s1, "删除bc后:"); PrintStringList(s2, "原s2串:"); s2.Insert(3, new char[] { '5', '2', '0' }); PrintStringList(s2, "在3号位插入520后:"); Console.WriteLine(); //复制操作 PrintStringList(s1, "原s1串:"); s1.CopyTo(2, s2); PrintStringList(s1, "复制s2整个字符串在2号位后:"); PrintStringList(s2, "原s2串:"); s2.CopyTo(1, new char[] { 'a', 'b', 'c', 'g', 'h' }, 3, 3); PrintStringList(s2, "复制cgh到1号位后:"); Console.WriteLine(); //链接串操作 PrintStringList(s1, "串1:"); PrintStringList(s2, "串2:"); StringList s3 = s1.ConcatToNew(s2); PrintStringList(s3, "链接s1和s2为s3后:"); Console.WriteLine(); //截取串操作 PrintStringList(s3, "s3串为:"); StringList s4 = s3.SubString(5, 8); PrintStringList(s4, "5到13的串为:"); Console.WriteLine(); //匹配字符串 PrintStringList(s3, "字符串s3为:"); Console.WriteLine("在s3中匹配s2的位置:"); Console.WriteLine("从1开始:"+s3.SimpleIndex(s2)); Console.WriteLine("从1开始:"+s3.Index(s2)); StringList match = new StringList(new char[] { '5', '2', '0' }); Console.WriteLine("在s3中匹配520的位置:"); Console.WriteLine("从8开始:"+s3.Index(match,8)); Console.WriteLine("从1开始:"+s3.SimpleIndex(match)); Console.WriteLine(); //索引错误测试 char c = s3[200]; s1.Insert(0, null); s3.CopyTo(-1, s4); } static void PrintStringList(StringList s, string text = "输出:") { Console.Write(text); for (int i = 1; i <= s.Length(); i++) { Console.Write(s[i]); } Console.WriteLine(); } |
结果