线性表的链式存储结构

发表评论
17,325 views

A+

所属分类：Fly数据结构与算法原创文章

上次实现了线性表的顺序存储结构

现在我们来实现线性表的链式存储结构

链式存储结构的特点是用一组任意的存储单元

存储线性表中的元素

可以是连续的也可以是不连续的

除了需要储存数据元素的信息外

还要存储它后继元素的内存地址

class MyLink<T>
{
    class Node{
        public T data;
        public Node next;
    }


    private Node _head;
    private Node _last;
    private int _curentLinkLength;

class MyLink<T>

{

class Node{

public T data;

public Node next;

}

private Node _head;

private Node _last;

private int _curentLinkLength;

首先，在类中抽象一个类出来丛当结点

data用于保存数据（数据域）

next用于指向下一个结点（指针域）

这样把一个一个结点串联起来

_head是头结点

_last是尾结点

_currentLinkLength是链表的长度

//构造函数，创建头结点，空链表
public MyLink() {
    _head = new Node();
    _head.next = null;
    _last = _head;
    this._curentLinkLength = 0;
}

//构造函数，创建头结点，空链表

public MyLink() {

_head = new Node();

_head.next = null;

_last = _head;

this._curentLinkLength = 0;

}

初始化链表为只有一个头结点的空链表

头结点是为了操作方便和同一而设立的

它没有正真的数据意义

它也不是链表的必须要素

//获取指定位置的节点
private Node GetNodeByIndex(int index)
{
    Node go = this._head;
    int i = 0;
    while (go != null && i < index)
    {
        go = go.next;
        i++;
    }

    if (i != index) go = null;

    return go;
}

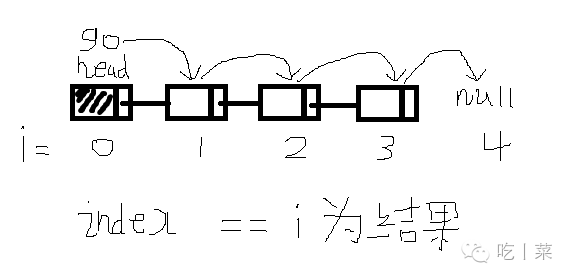
//获取指定位置的节点

private Node GetNodeByIndex(int index)

{

Node go = this._head;

int i = 0;

while (go != null && i < index)

{

go = go.next;

i++;

}

if (i != index) go = null;

return go;

}

获取链表中特定位置的节点

在链表操作中

添加、插入、删除等都需要获取到指定位置的结点

①初始化结点go为头结点，初始化i = 0

②当go不为空时和当前结点位置i小于目标位置index时

将go结点向后推移

③直到链表元素不够（go ==null）或者到达目标结点（i == index）

返回 go结点

（这里i的大小刚好对应第i个结点）

//获取链表中的第i位元素
public bool GetElement(int index, ref T element) {
    Node go = this.GetNodeByIndex(index);

    if (go == null||go == this._head)
    {
        Console.WriteLine("索引非法！");
        return false;
    }

    element = go.data;
    return true;
}

//获取链表中的第i位元素

public bool GetElement(int index, ref T element) {

Node go = this.GetNodeByIndex(index);

if (go == null||go == this._head)

{

Console.WriteLine("索引非法！");

return false;

}

element = go.data;

return true;

}

通过索引获取链表中的节点元素数据

①通过上面的方法，获取到对应索引的节点

②判断是否是空结点（索引超出了范围）或是为特殊结点头结点

③如果不是再取出数据

//向链表后面添加元素
public bool Add(T element) {
    Node last = _head;
    while (last.next != null) {
        last = last.next;
    }


    //此时last为链表的最后元素
    Node add = new Node();
    add.data = element;
    add.next = null;
    last.next = add;
    this._last = add;
    this._curentLinkLength++;

    return true;
}

//向链表后面添加元素

public bool Add(T element) {

Node last = _head;

while (last.next != null) {

last = last.next;

}

//此时last为链表的最后元素

Node add = new Node();

add.data = element;

add.next = null;

last.next = add;

this._last = add;

this._curentLinkLength++;

return true;

}

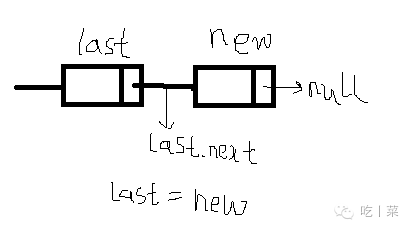
①要在链表中的最后面添加元素，先遍历链表找到最后一个结点

最后一个结点的next为空

②新建一个节点，赋值数据，指定next为空

③指定尾结点的next结点为新建结点

④指定尾结点为新建结点（用于快速添加）

⑤链表的长度+1

时间复杂度为O(n)

//向链表后面快速添加元素
public bool AddQuick(T element) {

    Node add = new Node();
    add.data = element;
    add.next = null;
            
    this._last.next = add;
    this._last = add;
    this._curentLinkLength++;
    return true;

}

//向链表后面快速添加元素

public bool AddQuick(T element) {

Node add = new Node();

add.data = element;

add.next = null;

this._last.next = add;

this._last = add;

this._curentLinkLength++;

return true;

}

文章的开始

我声明了一个变量引用的就是尾结点

通过这个尾结点我们可以快速地向链表后面添加元素

①新建一个结点，赋值数据，指定next为空

②直接使用已有的last，设置尾结点的下一个next结点为新建结点

③指定新建结点为尾结点

④链表长度+1

时间复杂度为O(1)

需要保存尾结点的引用，增加了内存（这是小事）

//向链表头部增加元素
public bool AddToHead(T element) {
    Node add = new Node();
    add.data = element;
    add.next = _head.next;
    if (_head.next == null) {
        //判断是否是空链表，如果是，尾结点就是插入结点
        this._last = add;
    }

    _head.next = add;
    this._curentLinkLength++;
    return true;
}

//向链表头部增加元素

public bool AddToHead(T element) {

Node add = new Node();

add.data = element;

add.next = _head.next;

if (_head.next == null) {

//判断是否是空链表，如果是，尾结点就是插入结点

this._last = add;

}

_head.next = add;

this._curentLinkLength++;

return true;

}

往链表头部添加元素

这时候头结点的作用就很大了

利用头结点可以轻松实现

①新建结点，赋值数据，指定第一个结点为新建结点的next个结点（新建结点为第一个）

②因为有尾结点的因素，需要判断一下是否为特殊情况的空链表

若果是则尾结点指定为新建的结点

③指定头结点的下一个结点为新节点（第一个）

④链表的长度+1

//向后批量增加元素
public bool AddVolume(T[] elements) {
    for (int i = 0; i < elements.Length; i++) {
        this.AddQuick(elements[i]);
    }

    return true;
}

//向后批量增加元素

public bool AddVolume(T[] elements) {

for (int i = 0; i < elements.Length; i++) {

this.AddQuick(elements[i]);

}

return true;

}

这个就不解释了

//向链表索引i前插入元素
public bool Insert(int index, T element) {
    Node go = this.GetNodeByIndex(index - 1);

    if (go == null || go.next == null)
    {
        Console.WriteLine("索引非法！");
        return false;
    }

    Node add = new Node();
    add.data = element;
    add.next = go.next;
    go.next = add;
    this._curentLinkLength++;

    return true;
}

//向链表索引i前插入元素

public bool Insert(int index, T element) {

Node go = this.GetNodeByIndex(index - 1);

if (go == null || go.next == null)

{

Console.WriteLine("索引非法！");

return false;

}

Node add = new Node();

add.data = element;

add.next = go.next;

go.next = add;

this._curentLinkLength++;

return true;

}

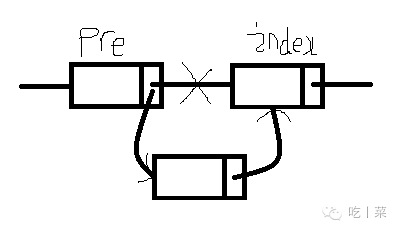
①找到需要插入位置结点的上一个结点

②判断这个结点时否符合（索引是否合法）

需要插入位置的结点i不能为空

③如果合法，则新建结点。赋值数据，指定next为待插入位置index的结点

就是上一个结点的next

④指定上一个结点的next结点为新建结点，完成插入

⑤链表长度+1

//批量插入元素
public bool InsertVolume(int index, T[] elements) {
    Node go = this.GetNodeByIndex(index - 1);
    if (go == null || go.next == null) {
        Console.WriteLine("索引非法!");
        return false;
    }
    for (int i = 0; i < elements.Length; i++) {
        Node add = new Node();
        add.data = elements[i];
        add.next = go.next;
        go.next = add;
        go = add;
        this._curentLinkLength++;
    }

    return true;
}

//批量插入元素

public bool InsertVolume(int index, T[] elements) {

Node go = this.GetNodeByIndex(index - 1);

if (go == null || go.next == null) {

Console.WriteLine("索引非法!");

return false;

}

for (int i = 0; i < elements.Length; i++) {

Node add = new Node();

add.data = elements[i];

add.next = go.next;

go.next = add;

go = add;

this._curentLinkLength++;

}

return true;

}

注意这里不同于批量添加

批量添加由于有尾结点的缘故

所以他可以直接调用快速添加

每次为O（1）

如果批量插入每次也调用插入方法的话

每次都要去查找到对应位置的结点

所以每次插入都为O（n）

这里：

①找到插入位置的上一个结点

②做出对结点和索引合法性的判断

③合法则遍历插入的每个元素，为每个元素创建一个新的结点

赋值结点的数据

指定下一个结点为被插入结点（go.next）

指定上一个结点的next为新建结点

线性表的长度+1

//通过索引删除元素
public T DeleteByIndex(int index) {
            

    Node go = this.GetNodeByIndex(index - 1);

    if (go == null || go.next == null) {
        Console.WriteLine("索引非法！");
        return default(T);
    }
            

    Node p = go.next;
    T old = p.data;
    go.next = p.next;
    p = null;

    if (index == this._curentLinkLength)
    {
        //说明删除的是最后一个元素
        this._last = go;
    }
    this._curentLinkLength--;
    return old;
}

//通过索引删除元素

public T DeleteByIndex(int index) {

Node go = this.GetNodeByIndex(index - 1);

if (go == null || go.next == null) {

Console.WriteLine("索引非法！");

return default(T);

}

Node p = go.next;

T old = p.data;

go.next = p.next;

p = null;

if (index == this._curentLinkLength)

{

//说明删除的是最后一个元素

this._last = go;

}

this._curentLinkLength--;

return old;

}

通过索引删除链表的对应结点

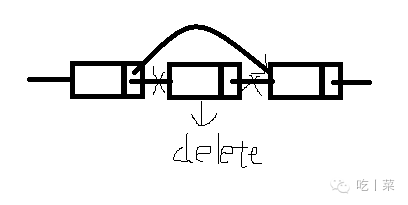
①找到要删除结点的上一个结点

②判断结点的合法性（索引的合法性）

③将将要删除的结点赋值给p，取出它的数据

④指定上一个结点的next为将要删除结点的下一个

⑤将删除结点p设为null

⑥判断一下被删除的结点是否为最后一个

若是，则将尾结点设为上一个结点go

⑦线性表的长度-1，返回被删除元素

//获取链表的长度
public int GetLinkLength() {
    return this._curentLinkLength;
}

//获取链表的长度

public int GetLinkLength() {

return this._curentLinkLength;

}

这个不用说

测试

static void TestLink() {

    //增加一个元素，删除两个元素
    MyLink<int> myLink = new MyLink<int>();
    myLink.Add(2);
    PrintLink(myLink, "增加一个元素后：");
    myLink.DeleteByIndex(1);
    PrintLink(myLink, "删除一个元素后：");
    myLink.DeleteByIndex(1);
    PrintLink(myLink, "再删除空链表的一个元素后：");
    Console.WriteLine();

    //快速增加元素与插入元素
    myLink.AddQuick(5);
    PrintLink(myLink, "快速添加3个元素后：");
    myLink.Insert(1, 80);
    PrintLink(myLink, "向索引1前插入80后：");
    myLink.DeleteByIndex(1);
    myLink.DeleteByIndex(1);
    PrintLink(myLink, "连续删除第一个元素后：");
    Console.WriteLine();

    //在头部添加两个元素，在快速插入一个
    myLink.AddToHead(20);
    PrintLink(myLink, "第一次在头部添加元素后：");
    myLink.AddToHead(10);
    PrintLink(myLink, "第二次在头部添加元素后：");
    myLink.AddQuick(30);
    PrintLink(myLink, "快速添加元素后：");
    myLink.DeleteByIndex(3);
    PrintLink(myLink, "删除第三个元素后：");
    myLink.AddQuick(5);
    PrintLink(myLink, "在快速添加元素5:");
    Console.WriteLine();

    //批量添加和插入元素
    int[] array = { 1, 3, 6 };
    myLink.AddVolume(array);
    PrintLink(myLink, "批量插入1,3,6后：");
    myLink.InsertVolume(2, array);
    PrintLink(myLink, "在索引2前批量插入1，3，6后：");
    myLink.Add(55);
    myLink.AddQuick(66);
    PrintLink(myLink, "添加55，和快速添加66后：");
    Console.WriteLine();

    //索引非法检测
    int data = 0;
    myLink.GetElement(0, ref data);
    myLink.GetElement(100, ref data);
    myLink.Insert(30, 20);
    myLink.DeleteByIndex(-1);
    myLink.DeleteByIndex(200);
}

static void PrintLink(MyLink<int> l, string text = "输出：") {
    int data = 0;

    Console.Write(text);
    for (int i = 0; i < l.GetLinkLength(); i++) {
        l.GetElement(i + 1, ref data);
        Console.Write(data.ToString() + " ");
    }
    Console.WriteLine();
}

static void TestLink() {

//增加一个元素，删除两个元素

MyLink<int> myLink = new MyLink<int>();

myLink.Add(2);

PrintLink(myLink, "增加一个元素后：");

myLink.DeleteByIndex(1);

PrintLink(myLink, "删除一个元素后：");

myLink.DeleteByIndex(1);

PrintLink(myLink, "再删除空链表的一个元素后：");

Console.WriteLine();

//快速增加元素与插入元素

myLink.AddQuick(5);

PrintLink(myLink, "快速添加3个元素后：");

myLink.Insert(1, 80);

PrintLink(myLink, "向索引1前插入80后：");

myLink.DeleteByIndex(1);

PrintLink(myLink, "连续删除第一个元素后：");

Console.WriteLine();

//在头部添加两个元素，在快速插入一个

myLink.AddToHead(20);

PrintLink(myLink, "第一次在头部添加元素后：");

myLink.AddToHead(10);

PrintLink(myLink, "第二次在头部添加元素后：");

myLink.AddQuick(30);

PrintLink(myLink, "快速添加元素后：");

myLink.DeleteByIndex(3);

PrintLink(myLink, "删除第三个元素后：");

myLink.AddQuick(5);

PrintLink(myLink, "在快速添加元素5:");

Console.WriteLine();

//批量添加和插入元素

int[] array = { 1, 3, 6 };

myLink.AddVolume(array);

PrintLink(myLink, "批量插入1,3,6后：");

myLink.InsertVolume(2, array);

PrintLink(myLink, "在索引2前批量插入1，3，6后：");

myLink.Add(55);

myLink.AddQuick(66);

PrintLink(myLink, "添加55，和快速添加66后：");

Console.WriteLine();

//索引非法检测

int data = 0;

myLink.GetElement(0, ref data);

myLink.GetElement(100, ref data);

myLink.Insert(30, 20);

myLink.DeleteByIndex(-1);

myLink.DeleteByIndex(200);

}

static void PrintLink(MyLink<int> l, string text = "输出：") {

int data = 0;

Console.Write(text);

for (int i = 0; i < l.GetLinkLength(); i++) {

l.GetElement(i + 1, ref data);

Console.Write(data.ToString() + " ");

}

Console.WriteLine();

}

结果

发表评论取消回复

登录 注册 找回密码

登录注册找回密码